If two planes intersect each other, the intersection will always be a line.
The vector equation for the line of intersection is given by
where . r_0. is a point on the line and . v. is the vector result of the cross product of the normal vectors of the two planes.
The parametric equations for the line of intersection are given by
where . a. . b. and . c. are the coefficients from the vector equation . r=a\bold i+b\bold j+c\bold k.
Example
Find the parametric equations for the line of intersection of the planes.
We need to find the vector equation of the line of intersection. In order to get it, we’ll need to first find . v. the cross product of the normal vectors of the given planes.
The normal vectors for the planes are
For the plane . 2x+y-z=3. the normal vector is . a\langle2,1,-1\rangle.
For the plane . x-y+z=3. the normal vector is . b\langle1,-1,1\rangle.
The cross product of the normal vectors is
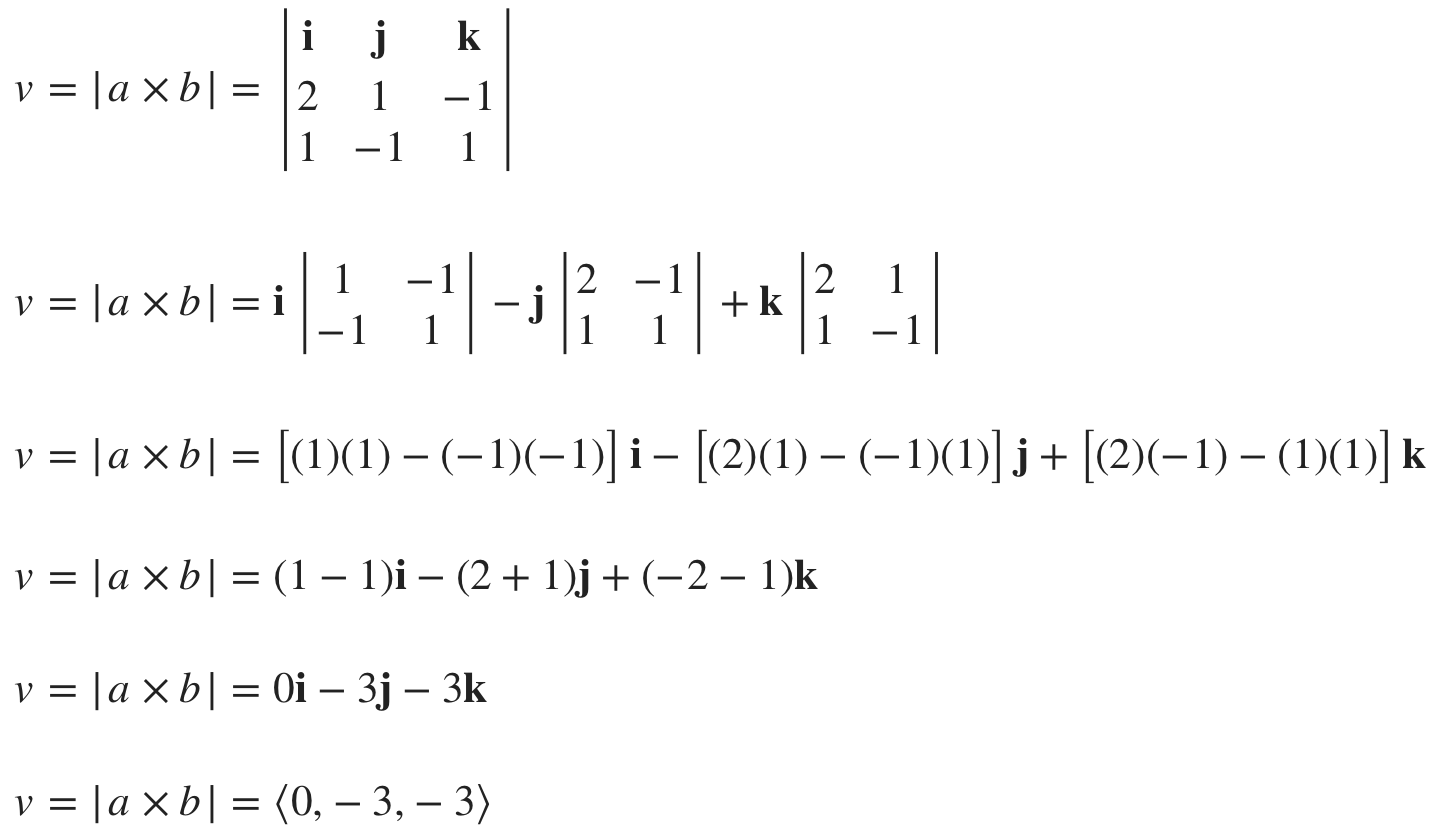
We also need a point on the line of intersection. To get it, we’ll use the equations of the given planes as a system of linear equations. If we set . z=0. in both equations, we get
intersection of two planes.jpg" width="1500" height="1500" />
Now we’ll add the equations together.
Plugging . x=2. back into . x-y=3. we get
Putting these values together, the point on the line of intersection is
. r_0=2\bold i-\bold j+0\bold k.
Now we’ll plug . v. and . r_0. into the vector equation.
. r=(2\bold i-\bold j+0\bold k)+t(0\bold i-3\bold j-3\bold k).
. r=2\bold i-\bold j+0\bold k+0\bold it-3\bold jt-3\bold kt.
. r=2\bold i-\bold j-3\bold jt-3\bold kt.
. r=(2)\bold i+(-1-3t)\bold j+(-3t)\bold k.
With the vector equation for the line of intersection in hand, we can find the parametric equations for the same line. Matching up . r=a\bold i+b\bold j+c\bold k. with our vector equation . r=(2)\bold i+(-1-3t)\bold j+(-3t)\bold k. we can say that
Therefore, the parametric equations for the line of intersection are
For integrals containing exponential functions, try using the power for the substitution.
